এই লেখাটিতে ইলেকট্রিক্যাল প্রয়োজনীয় সূত্র ও সার্কিট সম্বন্ধে ধারণা দিতে কিছু টপিক কাভার করার চেষ্টা করা হয়েছে। যে যে বিষয়গুলো যুক্ত করা হয়েছেঃ
- ভোল্টেজ ডিভাইডার
- কারেন্ট ডিভাইডার
- কারশফের সূত্র (Kirchhoff’s Law)
- রেজিস্ট্যান্সের সূত্র (Resistance Law)
- ওহমের সূত্র
- ফ্যারাডের ইলেকট্রোলাইসিস সূত্র
- লেন্জের সূত্র (Lenz’s law)
- থেভেনিন থিউরম (Thevenin Theorem)
- সুপার পজিশন থিউরম (Superposition Theorem)
- এ্যাম্পিয়ারস ল (Ampere’s Law)
- ফ্লেমিং এর লেফট হ্যান্ড রুল (Fleming’s Left Hand Rule)
- ফ্লেমিং এর রাইট হ্যান্ড রুল (Fleming’s Left Hand Rule)
- জুলের সূত্র (Joules Law)
ইলেকট্রিক্যাল প্রয়োজনীয় সূত্র
ভোল্টেজ ডিভাইডার (Voltage Divider)
ইলেকট্রনিক্স এর ক্ষেত্রে, ভোল্টেজ ডিভাইডার একটি প্যাসিভ লিনিয়ার সার্কিট যা আউটপুট ভোল্টেজ উৎপন্ন করে এবং ইহার ইনপুট ভোল্টেজেরই ভগ্নাংশ। ভোল্টেজ ডিভাইডার মানে ভোল্টেজ কে বিভক্ত করবে কম্পোনেন্টের মধ্যে।
- ভোল্টেজ ডিভাইডার ব্যবহার করার মাধ্যমে নির্দিষ্ট রেসিস্টরের ভোল্টেজ নির্ণয় করতে পারবো।
- ভোল্টেজ ডিভাইডার ব্যবহার করার জন্য রেজিস্টর সিরিজে সংযুক্ত রাখতে হবে।
নিচে একটি উদাহরণ দেওয়া হলোঃ
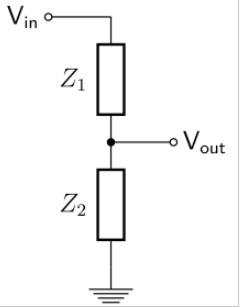
চিত্রে দুটি ইম্পিড্যান্স সিরিজে সংযুক্ত রয়েছে যেখানে সোর্স হিসেবে ইনপুট ভোল্টেজ রয়েছে এবং আউটপুট ভোল্টেজ Z1 ও Z2 এর মাঝামাঝিতে যুক্ত রয়েছে।
তাহলে,

কিংবা,
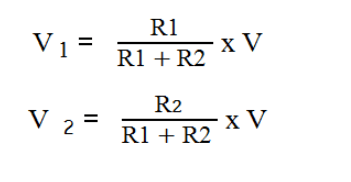
কারেন্ট ডিভাইডারঃ
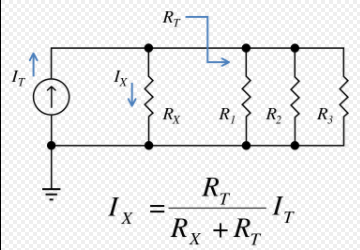
ইলেকট্রনিক্স এর ক্ষেত্রে কারেন্ট ডিভাইডার একটি সাধারণ লিনিয়ার সার্কিট যা আউটপুট কারেন্ট উৎপন্ন করে যা ইনপুট কারেন্টের ভগ্নাংশ। কারেন্ট ডিভাইডার মানে ব্রাঞ্চের মধ্য দিয়ে কারেন্টকে বিভক্ত করবে।
- কারেন্ট ডিভাইডার ব্যবহার করে নির্দিষ্ট রেজিস্টরের মধ্যে প্রবাহিত কারেন্টের মান নির্নয় করা যায়।
- কারেন্ট ডিভাইডার ব্যবহার করার জন্য রেজিস্টরদের প্যারালালে যুক্ত করতে হবে।
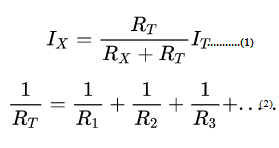
কার্শফের সূত্রঃ
ওহমের সূত্রের মাধ্যমে সরাসরি যে সমস্ত নেটওয়ার্ক এর সমাধান সম্ভব হয় না সেই সমস্ত নেটওয়ার্কের সমাধান কার্শফের সূত্রের মাধ্যমে করা সম্ভব। কার্শফের দুটি সূত্র রয়েছেঃ
- কার্শফের কারেন্ট সূত্র(KCL)
- কার্শফের ভোল্টেজ সূত্র(KVL)
১। কার্শফের কারেন্ট সূত্রঃ
কোন বৈদ্যুতিক নেটওয়ার্কের এক বিন্দুতে মিলিত কারেন্ট সমূহের বীজগানিতিক যোগফল শূন্য অথবা কোন বিন্দুতে আগত কারেন্ট = নির্গত কারেন্ট।
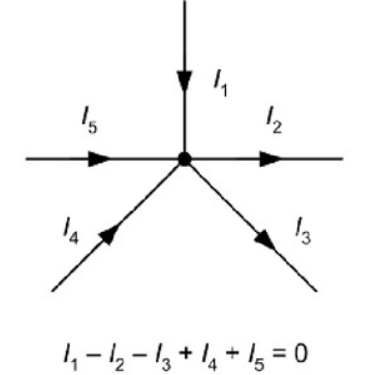
চিত্র হতে, ∑ I = 0
I1 – I2 – I3 + I4 + I5 = 0
২। কার্শফের ভোল্টেজ সূত্রঃ
কোন বদ্ধ বৈদ্যুতিক নেটওয়ার্কের সকল ই,এম,এফ এবং সকল ভোল্টেজ ড্রপের বীজগানিতিক যোগফল শূন্য।
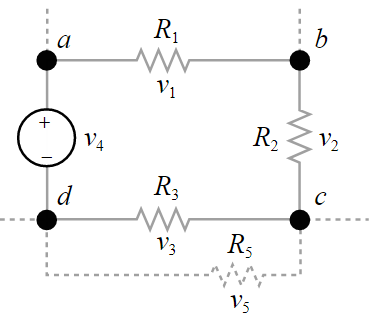
চিত্র হতে, v1 + v2 + v3 – v4 = 0
রেজিস্ট্যান্সের সূত্র (Resistance Law)
কোন নির্দিষ্ট তাপমাত্রায় একটি পরিবাহীর রেজিস্ট্যান্স দৈর্ঘ্যের সমানুপাতিক, প্রস্থের ব্যস্তানুপাতিক এবং এর রেজিস্ট্যান্স পরিবাহি পদার্থের আপেক্ষিক রোধের উপর নির্ভর করে।
R α L/A
R = ρL/A
এখানে,
R = রেজিস্ট্যান্স/রোধ।
ρ = স্পেসিফিক রেজিস্ট্যান্স/সমানুপাতিক ধ্রুবক।
L = দৈর্ঘ্য।
ওহমের সূত্র
নির্দিষ্ট তাপমাত্রায় কোন একটি পরিবাহির মধ্য দিয়ে প্রবাহিত কারেন্ট পরিবাহির দু প্রান্তের মধ্যকার বিভব পার্থক্যের সমানুপাতিক এবং রেজিস্ট্যান্সের ব্যাস্তানুপাতিক।
V α I
বা V = IR
যেখানে,
V = বিভিব পার্থক্য, I = কারেন্ট, R = পরিবাহির রেজিস্ট্যান্স
সীমাবদ্ধতাঃ
- এই সুত্রটি মূলত ডিসির ক্ষেত্রে প্রযোজ্য এসির জন্য নয়।
- তাপমাত্রা পরিবর্তন হলে ওহমের সূত্র প্রযোজ্য হবে না।
- তাপমাত্রা স্থির থাকলে সিলিকন কার্বাইডের ক্ষেত্রে ওহমের সূত্র প্রযোজ্য নয়।
- জটিল সার্কিট ওহমের সূত্রের সাহায্যে সমাধান করা যায় না।
ফ্যারাডের ইলেকট্রোলাইসিস সূত্র
বিজ্ঞানী মাইকেল ফ্যারাডে ইলেকট্রোলাইসিসের সূত্র দুটি উদ্ভাবন করেন
প্রথম সূত্র:
“ইলেকট্রোলাইসিস প্রক্রিয়ায় ইলেকট্রোডের উপর জমা হওয়া পদার্থের পরিমাণ, দ্রবণ বা ইলেকট্রোলাইটের ভিতর দিয়ে প্রবাহিত বিদ্যুতের পরিমাণের সমানুপাতিক”।
দ্বিতীয় সূত্র:
“ইলেকট্রোলাইসিস প্রক্রিয়ায় ইলেকট্রোডের উপর জমা হওয়া পদার্থের পরিমাণ এদের তড়িৎ রাসায়নিক সমতুলের সমানুপাতিক”।
প্রথম সূত্র অনুযায়ী m α q
দ্বিতীয় সূত্র অনুযায়ী m α Z
যেখানে,
q = চার্জ।
i = প্রবাহিত কারেন্ট
t = কারেন্ট প্রবাহের সময়
Z = পদর্থের তড়িৎ রাসায়নিক সমতুল
লেন্জের সূত্র (Lenz’s law)
লেনজের সূত্র মূলত হেনরিক লেনজের নামনুসারে রাখা হয়েছে।
“একটি প্রবর্তিত তড়িচ্চালক বল সব সময় তড়িৎকে বৃদ্ধি করে যার চুম্বকীয় ক্ষেত্র প্রকৃত চুম্বক প্রবাহের বিরোধিতা করে”
∈ = dΦB / -dt
এর থেকে বুঝা যায় যে আবেশিত তড়িচ্চালক বল (ℰ) এবং চুম্বকীয় প্রবাহ (∂ΦB) এর মধ্যে বিপরীত চিহ্ন আছে।
থেভেনিন থিউরম (Thevenin Theorem)
“ই.এম.এফ. এর একাধিক উৎস এবং রেজিস্ট্যান্স সমন্বয়ে গঠিত একটি জটিল নেটওয়ার্কের দুটি বিন্দুতে সংযুক্ত একটি লোড রেজিস্ট্যান্সের কারেন্ট একই হবে, যদি লোডটি ই.এম.এফ. এর একটি মাত্র স্থির উৎসের সাথে সংযুক্ত থাকে।
যার ই.এম.এফ. লোডের প্যারালেলে অপেন সার্কিট ভোল্টেজের সমান এবং যার ইন্টারনাল রেজিস্ট্যান্স দুটি প্রান্ত হতে বিপরীত দিকের নেটওয়ার্কের রেজিস্ট্যান্টের সমান। ই.এম.এফ. এর উৎসগুলো এদের সমতুল্য ইন্টারনাল রেজিস্ট্যান্সে স্থলাভিষিক্ত হবে”
সুপার পজিশন থিউরম (Superposition Theorem)
“কোন লিনিয়ার বাইলেটারাল নেটওয়ার্কে একটি বিন্দুতে প্রবাহিত কারেন্ট বা দুটি বিন্দুতে ই.এম.এফ. এর একাধিক উৎসের কারণে ঐ বিন্দু বা বিন্দুগুলোতে প্রবাহিত আলাদা আলাদা কারেন্ট সমুহের বা ই.এম.এফ. পার্থক্য সমুহের বীজগাণিতিক যোগফল সমান হবে যদি প্রতিটি উৎসকে আলাদা আলাদা ভাবে বিবেচনা করা হয় এবং অন্য উৎস গুলোর প্রতিটি সমমানের ইন্টারনাল রেজিস্ট্যান্সে রূপান্তর করা হয়”
এ্যাম্পিয়ারস ল (Ampere’s Law)
“কারেন্টবাহী দুটি সমান্তরাল পরিবাহীর মধ্যে ক্রিয়াশীল বল পরিবাহী দুইটির দৈর্ঘ্য এবং এদের মধ্যদিয়ে প্রবাহীত কারেন্টের গুণফলের সমানুপাতিক এবং পরিবাহী দুইটির মধ্যকার দূরত্বের ব্যস্তানুপাতিক”
তবে, F α I1I2L/r________(ইলেকট্রিক্যাল প্রয়োজনীয় সূত্র)
বা, F = 2X10-7I1I2L/r
এখানে,
বল F, কারেন্ট I1 ও I2, পরিবাহী দুটির দৈর্ঘ্য L, পরিবাহী দুইটির মধ্যকার দূরত্ব r
এখানে, 2X10-7= সমানুপাতিক ধ্রুবক
ফ্লেমিং এর লেফট হ্যান্ড রুল (Fleming’s Left Hand Rule)
“বাম হাতের বৃদ্ধাঙ্গুলি, তর্জনী ও মধ্যমাকে পরস্পর সমকোণে রেখে বিস্তৃত করলে, তর্জনী চুম্বক বলরেখার দিক ও মধ্যমা কারেন্টের দিক নির্দেশ করবে, বৃদ্ধাঙ্গুলি পরিবাহী তারের ঘূর্ণন দিক নির্দেশ করবে” মোটরের ঘূর্ণন দিক এই সূত্রের সাহায্যে বের করা যায়।
ফ্লেমিং এর রাইট হ্যান্ড রুল (Fleming’s Left Hand Rule)
“দক্ষিণ হস্তের বৃদ্ধাঙ্গুলি, তর্জনী ও মধ্যমাকে পরস্পর সমকোণে রেখে বিস্তৃত করলে যদি তর্জনী চৌম্বক বলরেখার অভিমুখ এবং বৃদ্ধাঙ্গুলি পরিবাহী তারের ঘূর্ণনের অভিমুখ নির্দেশ করে, তবে মধ্যমা পরিবাহিতে প্রবাহিত আবেশিত কারেন্টের অভিমুখ নির্দেশ করেবে। ইহাই ফ্লেমিং এর রাইট হ্যান্ড রুল”
জুলের সূত্র (Joules Law)
“যদি তাপকে H, কারেন্টকে I, রেজিস্ট্যান্সকে R এবং সময় কে t দিয়ে প্রকাশ করা হয়, তবে গানিতিক ভাবে লেখা যায়ঃ
১. H α I2, যখন R এবং t ধ্রুব
২. H α R, যখন I এবং t ধ্রুব
৩. H α t, যখন I এবং R ধ্রুব
অতএব, H α I2Rt” বা H=I2RT/J
এখনে, J = 4200 জুল/কিলো ক্যালোরি মেকানিক্যাল ইকুভেলেন্ট অফ হিট (সমানুপাতিক ধ্রুবক), ।(ইলেকট্রিক্যাল প্রয়োজনীয় সূত্র)