কার্শফের সূত্র – ১ : কার্শফের কারেন্ট সূত্র | KCL – Kirchhoff’s Current Law

মাঝে মাঝে আমরা এমন কিছু সার্কিটের মুখোমুখি হই যা ওহমের সূত্র বা অন্যান্য সূত্রের সাহায্যে সমাধান করা সম্ভব হয় না। তখন আমাদের বিশেষ কিছু সূত্রের সাহায্য নিতে হয়। কার্শফের সূত্র সমূহ হচ্ছে সেই বিশেষ সূত্র সমূহ যার সাহায্যে অনেক জটিল সার্কিট সমাধান করা যায়।

আলোচনার সুবিধার্থে কার্শফের সূত্র সম্পর্কিত আলোচনাকে আমরা মোট দুইটি অংশে বিভক্ত করেছি।

আজ তার প্রথম অংশ ।

প্রথম অংশে যা যা থাকছেঃ

• প্রাথমিক জ্ঞান।
• কার্শফের সূত্র সমুহ।
• কার্শফের কারেন্ট সূত্র বা KCL
• কার্শফের কারেন্ট সূত্রের ব্যাখ্য।
• কার্শফের কারেন্ট সূত্রের সাহায্যে সমাধান করার কৌশল।
• কার্শফের কারেন্ট সূত্রের সাহায্যে প্রশ্ন সমাধান।

প্রাথমিক জ্ঞানঃ  

কার্শফের সূত্র কি তা শুরু করার আগে আমাদেরকে নোড, ব্রাঞ্চ ও লুপ কি তা মনে রাখতে হবে। নয়তো কার্শফের সূত্র সমূহ সঠিক ভাবে বুঝা যাবে না।

নোড, ব্রাঞ্চ, লুপ, মেশ সম্বন্ধে পড়ুন

কার্শফের সূত্র সমুহঃ

১৮৪৭ সালে জার্মান পদার্থ বিজ্ঞানী গুস্তাভ রবার্ট কার্শফ (Gustav Robert Kirchhoff) ভোল্টেজ ও কারেন্ট সম্পর্কিত দুইটি সূত্র প্রকাশ করেন।

তার সূত্র দুইটি হচ্ছে-

1. কার্শফের কারেন্ট সূত্র (Kirchhoff’s Current Law) বা KCL.
2. কার্শফের ভোল্টেজ সূত্র (Kirchhoff’s Voltage Law) বা KVL

কার্শফের সূত্র ব্যবহার করে কোনো সার্কিটে অজানা কারেন্টের মান বের করা যায়।

কার্শফের কারেন্ট সূত্র (Kirchhoff Current Law) বা KCL :

কার্শফ তার কারেন্ট সূত্রে বলেছিলেন যে,

“কোন নোডে প্রবেশ করা কারেন্টের যোগফল নোড হতে বাহির হওয়া কারেন্টের যোগফলের সমান”।

অর্থাৎ, নোডে মিলিত কারেন্ট সমূহের বীজগাণিতিক যোগাফল শূন্য।

সূত্র অনুসারে, নোডে আগত কারেন্ট = নোড হতে নির্গত কারেন্ট

বা, Iin = Iout

বা,‌‍ Σ I = 0

কার্শফের কারেন্ট সূত্রের ব্যাখ্যাঃ

আমরা নিচের চিত্রটির আলোকে কার্শফের কারেন্ট সূত্র ব্যাখ্যা করবো।

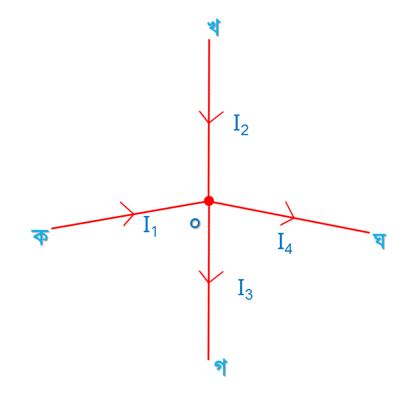
উপরের চিত্রে ৪ টি কন্ডাকটর বা পরিবাহী রয়েছে যা যথাক্রমে ক, খ, গ ও ঘ দ্বারা চিহ্নিত করা হয়েছে এবং এসব পরবাহী ০ বিন্দুতে মিলিত অবস্থায় রয়েছে। এই ৪ টি পরিবাহীর মধ্য দিয়ে যথাক্রমে I₁, I₂, I₃ ও I₄ কারেন্ট প্রবাহিত হচ্ছে। চিত্রে তীর চিহ্ন দ্বারা এদের ডিরেকশন চিহ্নিত করা হয়েছে। লক্ষ্য করে দেখুন, ক ও খ এর কারেন্ট I₁ ও I₂ এর ০ বিন্দুতে প্রবেশ করছে, আবার গ ও ঘ কারেন্ট I₃ ও I₄ ০ বিন্দু হতে বের হয়ে যাচ্ছে।

এখানে, আগত কারেন্টের মান পজিটিভ হলে নির্গত কারেন্টের মান নেগেটিভ হবে। কার্শফের কারেন্ট সূত্র অনুসারে আমরা লিখতে পারি,

I₁ + I₂ + (-I₃) + (-I₄) = 0

বা, I₁ + I₂ = I₃ + I₄

অর্থাৎ, আগত কারেন্ট = নির্গত কারেন্ট।

মূল কথা হচ্ছে, নোডে কোন কারেন্ট জমা থাকে না৷ যে পরিমাণ কারেন্ট আসে ঠিক সেই পরিমাণ কারেন্ট আবার চলে যায়।

কার্শফের কারেন্ট সূত্রের মাধ্যমে সমাধানের কৌশলঃ

নোডে যদি কারেন্ট প্রবেশ করে তবে তা পজিটিভ বা যোগ বোধক হবে এবং নোড হতে যদি কারেন্ট বের হয়ে যায় তবে তা নেগেটিভ বা বিয়োগ বোধক হবে।

নিচের প্রশ্নটি সমাধান করার পর বিষয়টি আরো ক্লিয়ার হবে।

কার্শফের কারেন্ট সূত্রের সাহায্যে প্রশ্ন সমাধানঃ

প্রশ্নঃ নিচের চিত্রে একটি নোড দেখানো হয়েছে। এই নোডের তিন বাহুতে 3 A, 4 A ও 2 A কারেন্ট দেখানো হয়েছে। নোড হতে কারেন্টের পরিমাণ নির্ণয় কর।

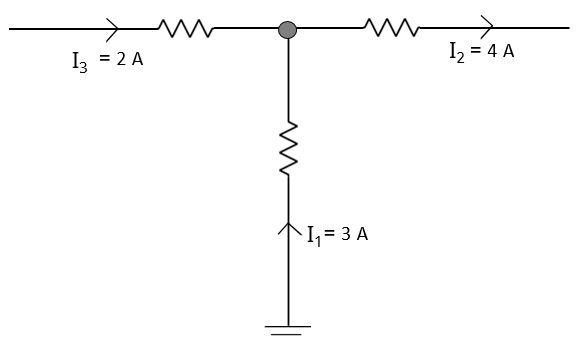
সমাধানঃ মনে করি,

I₁ =3 A

I₂ = 4 A

এবং I₃ = 2 A

চিত্র হতে দেখতে পাচ্ছি যে,  I₁ ও I₃ কারেন্ট নোডে প্রবেশ করছে। সুতরাং তারা যোগ বোধক হবে অর্থাৎ, +I₁ ও +I₃. আবার দেখা যাচ্ছে কারেন্ট I₂ নোড হতে বের হয়ে যাচ্ছে। সুতরাং তারা বিয়োগ বোধক হবে অর্থাৎ, -I₂.

এখন যদি একে সমীকরণ আকারে সাজাই তাহলে হবে,

+ I₁ + I₃ – I₂ = 0

বা, 3 + 2 – 4 = 0

বা, 5 – 4= 0

বা, 1 A

সুতরাং এই নোডে 1 A কারেন্ট আছে।

(ans).

ইলেকট্রিক্যাল প্রয়োজনীয় সূত্র যা আপনার জেনে রাখা উচিত পড়ুন

ওহমের সূত্র নিয়ে বিস্তারিত আলোচনা পড়ুন