কার্শফের সূত্র – ২ : কার্শফের ভোল্টেজ সূত্র | KVL – Kirchhoff’s Voltage Law

কার্শফের কারেন্ট সূত্রের মতই কার্শফের ভোল্টেজ সূত্র অনেক গুরুত্বপুর্ণ। এই দুই সূত্র এবং ওহমের সূত্র মিলে ইলেকট্রিক্যাল সার্কিট থিওরির ভিত্তি তৈরি হয়। তাই কোন সার্কিটকে বুঝতে হলে অবশ্যই এই তিনটা সূত্র খুব ভালোভাবে বুঝতে হবে।

"কার্শফের সূত্র - ১ : কার্শফের কারেন্ট সূত্র"

"ওহমের সূত্র নিয়ে বিস্তারিত আলোচনা"

কার্শফ সূত্র সম্পর্কিত আলোচনাকে আমরা মোট দুইটি অংশে ভাগ করেছিলাম। আজ তার ২য় বা শেষ অংশ।

আজকের আলোচনায় যা যা থাকছেঃ

• কার্শফের ভোল্টেজ সূত্র।
• কার্শফের ভোল্টেজ সূত্র সমাধান করার কৌশল ও ব্যাখ্যা।
• কার্শফের ভোল্টেজ সূত্রের সাহায্যে সার্কিট সমাধান।

কার্শফের ভোল্টেজ সূত্রঃ

কার্শফ তার ভোল্টেজ সূত্রে বলেছিলেন যে,

কোন ক্লোজড লুপে উপস্থিত সবগুলো ভোল্টেজের বীজগাণিতিক যোগফল শূন্য হবে।

অর্থাৎ, ক্লোজড লুপের ভিতরে যে পরিমাণ ভোল্টেজের থাকবে তাদেরকে বীজগাণিতিক ভাবে সমাধান করলে তাদের যোগফল শূন্য হবে।

আমরা এভাবেও বলতে পারি যে, ক্লোজড লুপের ভিতরে যে পরিমাণ ভোল্টেজের পরিবর্তন হয় তার পরিমাণ শূন্য।

অর্থাৎ, ভোল্টেজের পরিবর্তন, ΔV = 0.

কার্শফের ভোল্টেজ সূত্র প্রয়োগ করার সময় ভোল্টেজ গুলোকে ক্লক ওয়াইজ (ঘড়ির কাটার দিকে) অথবা কাউন্টার ক্লক ওয়াইজ (ঘড়ির কাটার বিপরীত দিকে) ধরে নিতে হয়।   

কার্শফের ভোল্টেজ সূত্র (KVL) সমাধান করার কৌশল ও ব্যাখ্যাঃ

সমাধানের সময় প্রথমে সার্কিটের একটি ক্লোজড লুপকে ক্লক ওয়াইজ বা কাউন্টার ক্লক নিতে হবে। তারপর একটি ব্রাঞ্চ থেকে যাত্রা শুরু করে লুপ অনুযায়ী অগ্রসর হতে হবে। যদি লুপ ডিরেকশন এবং ভোল্টেজ সোর্স এর পজিটিভ দিক যদি একই দিকে হয় তখন সেই সোর্সকে নেগেটিভ হিসেবে ধরতে হবে৷ আবার যদি লুপ ডিরেকশন এবং ভোল্টেজ সোর্স এর নেগেটিভ দিক একই দিকে হয় তখন সেই সোর্সকে পজিটিভ হিসেবে ধরতে হবে।

যেমনঃ যদি কোন রেজিস্ট্যান্স আড়াআড়ি ভাবে ভোল্টেজ ড্রপ এর ক্ষেত্রে লুপ ডিরেকশন এবং কারেন্ট ডিরেকশন একই দিকে হয় তাহলে এই রেজিস্ট্যান্সের ভোল্টেজ ড্রপ নেগেটিভ হবে। আবার লুপ ডিরেকশন এবং কারেন্ট ডিরেকশন যদি বিপরীত দিকে হয় তাহলে এই রেজিস্ট্যান্সের ভোল্টেজ ড্রপ পজিটিভ হবে।

নিচের উদাহরণের সাহায্যে এ বিষয়টি আরেকটু ভালোভাবে বোঝা যাবে।

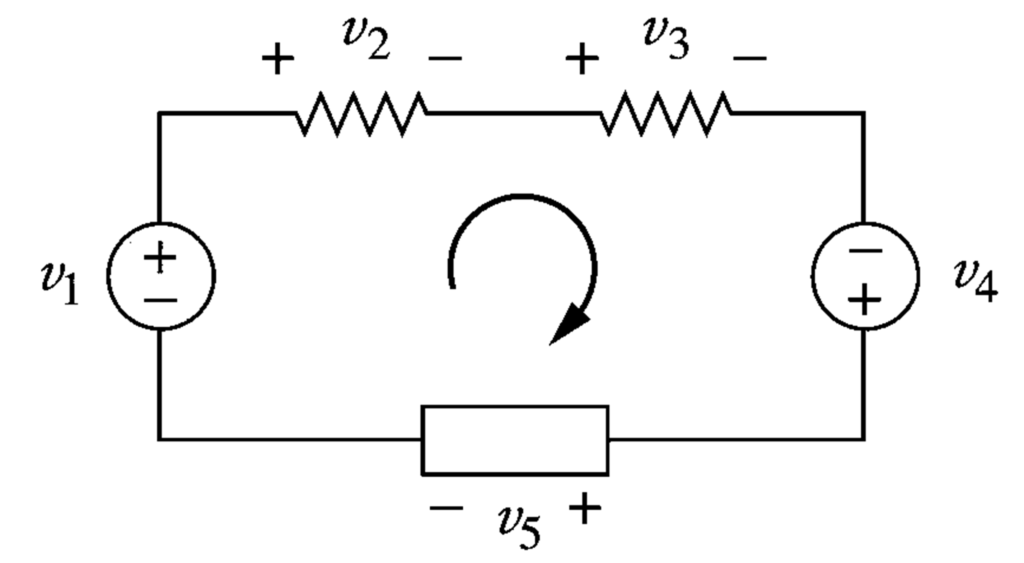
আমরা যদি উপরের সার্কিটে ক্লক ওয়াইজ লুপ ধরি তাহলে সার্কিট হতে যে সব ভোল্টেজ পাবো তা হলো,

-V₁, +V₂, +V₃, –V₄ এবং +V₅

উদাহরণ স্বরুপ, আমরা যদি ৩ নাম্বার ব্রাঞ্চ হতে যাত্রা শুরু করি তাহলে আমরা প্রথমে একটা পজিটিভ টার্মিনাল দেখতে পাবো আর তা হচ্ছে +V_{3 ,} যদি ৪ নাম্বার ব্রাঞ্চ হতে শুরু করি তাহলে একটা নেগেটিভ টার্মিনাল –V₄  পাবো। একইভাবে আমরা যদি উপরের সার্কিটে কার্শফের ভোল্টেজ সূত্র প্রয়োগ করি তাহলে পাবো,

-V₁ + V₂ + V₃ – V₄ + V₅ = 0

পুনর্বিন্যাস করলে পাই,

V₂ + V₃ + V₅ = V₁ + V₄

অর্থাৎ, ভোল্টেজ ড্রপ = ভোল্টেজ Rise

সুতরাং বলতে পারি যে, ক্লোজড লুপের ভিতরে যে পরিমাণ ভোল্টেজ বাড়ে ঠিক সে পরিমান ভোল্টেজ কমে যায় যার ফলে যোগফল শূন্য হয়।

কোন সার্কিটে কার্শফের ভোল্টেজ সূত্র প্রয়োগ করে খুব সহজেই ভোল্টেজ ড্রপ বের করা যায়।

কার্শফের ভোল্টেজ সূত্রের সাহায্যে সার্কিট সমাধানঃ

প্রথমে আমরা খুব সিম্পল একটা সার্কিট সমাধান করবো।

প্রশ্ন ১ঃ নিচের সার্কিট হতে V₃ বের করো।

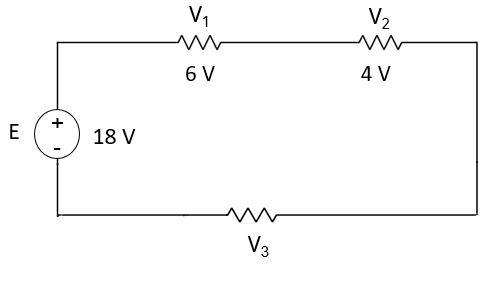
সমাধানঃ

দেওয়া আছে,

E = 18 V

V₁ = 6 V

V₂ = 4 V

V₃ = ?

আমরা যদি লুপকে ক্লক ওয়াইজ ধরি তাহলে সার্কিটটি নিম্ন রূপ হবে-

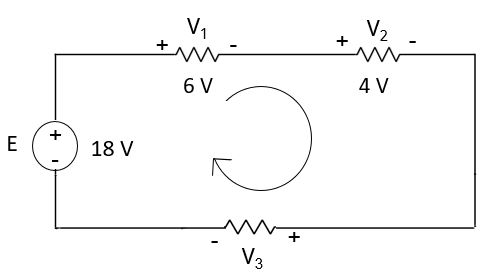
এবার সার্কিটে KVL এপ্লাই করলে পাই,

    -E + V₁ + V₂ + V₃ = 0

Or, -18 V + 6 V + 4 V + V₃ = 0

Or, -18 V + 10 V + V₃ = 0

Or, V₃ = 18 V – 10 V

 .·. V₃ = 8 V (উত্তর) ।

এবার আমরা একটু ভিন্ন রকম আরেকটি সার্কিট সমাধান করবো।

প্রশ্ন ২ঃ নিচের সার্কিটে একটি লুপ দেখানো হলো। এই লুপ হতে I₁ এবং I₂ এর মান বের করো।

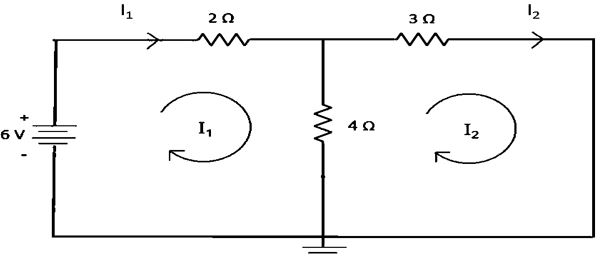
সমাধানঃ

অংকটি সমাধানের জন্য আমরা চিত্রের মতো দুইটি তীর চিহ্ন আকি এবং তীর চিহ্নকে I₁, I₂ হিসেবে চিহ্নিত করি।

এখন লুপ I₁ ধরে এগোতে থাকব।

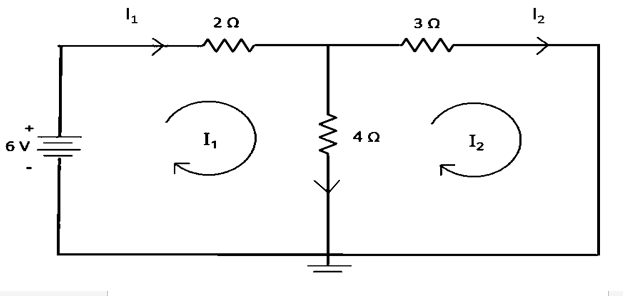
প্রথমে আমাদের সামনে পড়লো একটি ভোল্টেজ সোর্স (ব্যাটারি) যার মান ৬ ভোল্ট। কিন্তু এখানে লুপ ডিরেকশন ব্যটারির নেগেটিভ প্রান্ত দিয়ে প্রবেশ করে পজিটিভ প্রান্ত দিয়ে বের হয়েছে। তাই আমরা লিখবো – 6 V. এরপরই আমাদের পথে আছে ২ ওহম রেজিস্টর। 

ওহমের সূত্র হতে আমরা জানি, V = IR.

এখানে,

R = 2 ওহম এবং I = I₁.

সুতরাং, ভোল্টেজ V = I * R

= 2 I₁.

এরপর আছে আরেকটি ৪ ওহমের রেজিস্টর। একে লেখা যায় 4 I₁.

কিন্তু লক্ষ্য করলে দেখা যাবে, ৪ ওহম রেজিস্টরের ভিতর দিয়ে I₂ কারেন্ট বিপরীত দিকে প্রবাহিত হচ্ছে। তাই ৪ ওহম রেজিস্টরের ভোল্টেজ হবে,

4I₁ – 4I₂

= 4(I₁ – I₂).

এখন I₁ চিহ্নের পাশে আর কিছু নাই। এখন আমরা I₁ লুপের সমীকরণকে নিম্নোক্ত ভাবে লিখতে পারি,

-6V + 2I₁ + 4(I₁ – I₂)

Or, -6V + 2I₁ + 4I₁ – 4I₂

Or, -6V + 6I₁ – 4I₂ ………….. (১)

এবার আমাদেরকে লুপ I₂ ধরে এগোতে হবে।

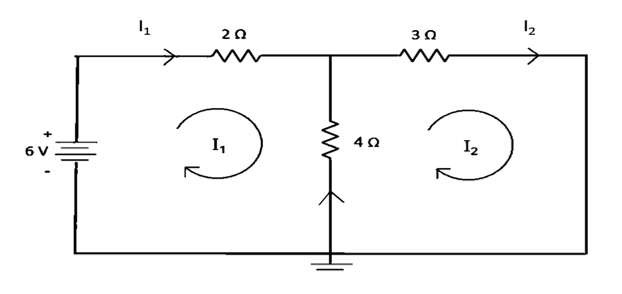
I₂ চিহ্ন থেকে শুরু করলে প্রথম আসে, ৩ ওহম রেজিস্টর। একে লিখতে হবে, 3 I₂. একইভাবে ৪ ওহম রেজিস্টরের জন্য লিখতে হবে, 4I₂ – 4I₁ = 4 (I₂ – I₁).

এবার I₂ লুপের সমীকরণকে নিম্নোক্তভাবে লিখতে পারি,

3 I₂ + 4 (I₂ – I₁).

Or, 3 I₂ + 4 I₂ – 4 I₁

Or, 7 I₂ – 4 I₁ ……….. (২)

এবার আমরা সমীকরণ দুইটিকে সমাধান করবো। এক্ষেত্রে সমীকরণ (১) কে 2 দিয়ে এবং সমীকরণ (২) কে 3 দিয়ে গুন করে বিয়োগ করলে পাই,

0 + I3 I2 = I2

Or, I2 = 12/13

Or, I₂ = 0.9 A.

এবার, I₂ এর মান ১ নং সমীকরণে বসালে পাই,

I₂ I₁ – 8 × 0.9 = 12

Or, I₂ I₁ – 7.2 = 12

Or, I₁ = (1₂ – 7.2) / 12

Or, I₁ = 0.4 A.

অতএব, I₂ = 0.9 A এবং I₁ = 0.4 A (উত্তর)