নরটন থিউরেম / নর্টন থিউরেমঃ কমপ্লেক্স সার্কিট সমাধান করার জন্য থেভেনিন’স থিওরেম এর পাশাপাশি নর্টন’স থিওরেমও বেশ জনপ্রিয় একটি পদ্ধতি। আমরা ইতিপূর্বে থেভেনিন’স থিওরেম নিয়ে বিস্তারিত আলোচনা করেছি। আজ আমরা নর্টন থিওরেম নিয়ে বিস্তারিত আলোচনা করব।
থেভেনিন থিওরেম সম্বন্ধে বিস্তারিত পড়ুন।
আমাদের আজকের আলোচনায় যা যা থাকছেঃ
- নর্টন’স থিওরেম / নরটন থিউরেম আবিষ্কার নিয়ে কিছু কথা।
- নরটন থিউরেম / নর্টন’স থিওরেম বিবৃতি।
- নরটন থিউরেম / নর্টন’স থিওরেম প্রয়োগ করার ধাপ সমূহ।
- নরটন থিউরেম / নর্টন’স থিওরেম এর সাহায্যে সার্কিট সমাধান।
নর্টন’স থিওরেম আবিষ্কার নিয়ে কিছু কথাঃ
এডওয়ার্ড লাওরী নর্টন (Edward L. Norton) বেল ল্যাবে যখন থেভেনিন থিওরেম নিয়ে গবেষণা করছিলেন তখন দেখতে পেলেন যে, একটি কমপ্লেক্স সার্কিটকে কারেন্ট সোর্স ও প্যারালাল রেজিস্ট্যান্সের মাধ্যমেও প্রকাশ করা যায়।
বিভিন্ন পরিক্ষা নীরিক্ষার পর অবশেষে তিনি ১৯২৬ সালে অর্থাৎ থেভেনিন’স থিওরেম আবিস্কারের প্রায় ৪৩ বছর পরে তার এ থিওরেমটি প্রকাশ করেন। কিন্তু দুঃখের বিষয় ঐ বছরই থেভেনিন থিওরেম এর আবিস্কারক লিওন চার্লস থেভেনিন (Léon Charles Thévenin)মৃত্যু বরণ করেন যার ফলে তার পক্ষ থেকে নর্টন’স থিওরেম সম্বন্ধে কোন মন্তব্য জানা যায় নি।
নর্টন থিওরেম বিবৃতিঃ
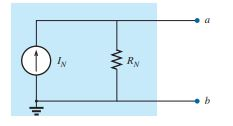
নর্টন তার থিওরেমে বলেছিলেন যে, “Any two-terminal linear bilateral dc network can be replaced by an equivalent circuit consisting of a current source and a parallel resistor“.
অর্থাৎ, যে কোন দ্বি-টার্মিনাল লিনিয়ার বাই লেটারাল ডি.সি নেটওয়ার্ক একটি equivalent circuit এর মাধ্যমে প্রকাশিত হতে পারে যা সাধারণত একটি কারেন্ট সোর্স এবং প্যারালাল রেজিস্টর এর সমন্বয়ে গঠিত। (সার্কিট ১)
নর্টন থিওরেম প্রয়োগ করার ধাপ সমূহঃ
নর্টন থিওরেম এর সাহায্যে কোন সার্কিটকে সমাধান করতে হলে আমাদেরকে কিছু ধাপ বা Steps অনুসরণ করতে হয়। ব্যাখ্যার সুবিধার্থে আমরা ধরে নেই নিম্নের সার্কিট হতে RL এর মধ্য দিয়ে প্রবাহিত কারেন্ট বের করতে হবে।
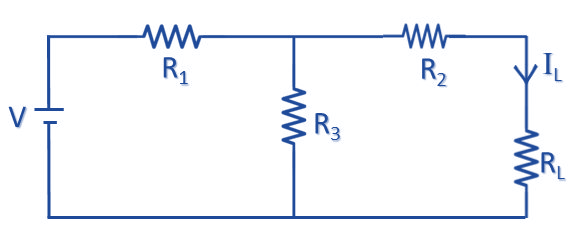
তাহলে এবার চলুন আমরা উপরের সার্কিটকে নর্টন থিওরেম এর সাহায্যে সমাধান করতে করতে সমাধান করার ধাপ বা Steps সমুহ জেনে নেইঃ
Step 1: প্রথমে যে লোড এর মধ্যে কারেন্ট বের করতে হবে সেই লোডটি শর্ট করে দিতে হবে। (চিত্র ২)
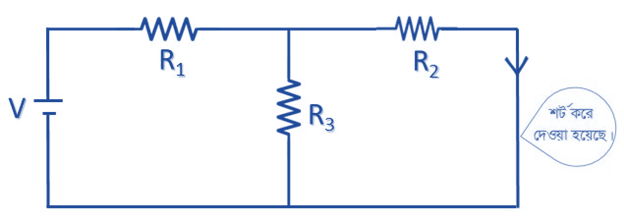
Step 2: যেই পথ শর্ট করা হয়েছে ঐ পথ দিয়ে প্রবাহিত Norton Current (IN) বের করতে হবে।
Step 3: এবার ঐ শর্ট পথটি খুলে ফেলতে হবে। ভোল্টেজ সোর্স থাকলে শর্ট করতে হবে এবং কারেন্ট সোর্স থাকলে ওপেন করতে হবে। এরপর এই সার্কিট হতে Norton Resistance (RN) বের করতে হবে।
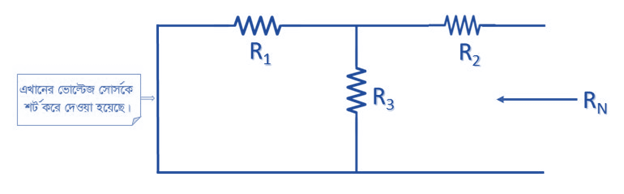
Step 4: সর্বশেষ IN, RN ও RL এর সমন্বয়ে Norton’s Equivalent Circuit অংকন করতে হবে এবং এই নতুন সার্কিট হতে IL এর মান নির্ণয় করতে হবে।
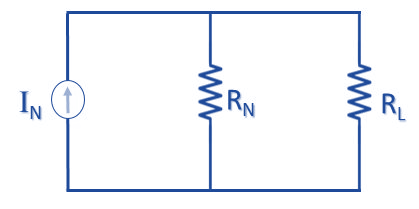
লোড কারেন্ট, IL = (RN×IN / RN+RL)
নর্টন থিওরেম এর সাহায্যে সার্কিট সমাধানঃ
প্রশ্নঃ নর্টন থিওরেম ব্যবহার করে নিম্নের সার্কিট হতে a b টার্মিনালে Norton’s Equivalent Circuit অংকন করো।
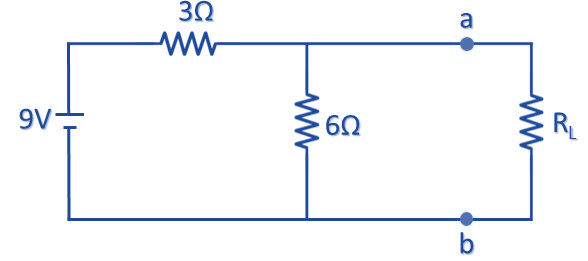
সমাধানঃ
প্রথমে আমরা a b টার্মিনালের RL কে শর্ট করে দিলাম।
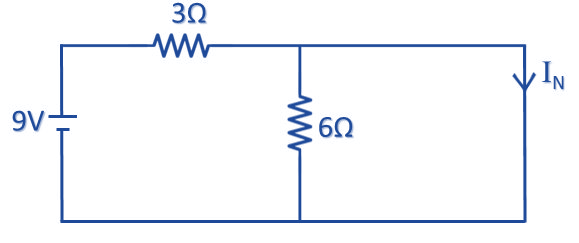
এবার এই পথ দিয়ে প্রবাহিত Norton Current (IN) বের করব,
.·. IN = 9 / 3 = 3 Amps.
এরপর IN শর্ট পথটি ওপেন করে এবং 9 V যুক্ত ভোল্টেজ সোর্সকে শর্ট করে নিম্নের সার্কিট হতে Norton Resistance (RN) বের করতে হবে,
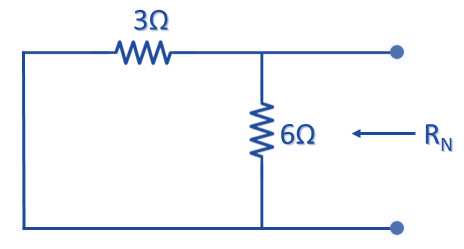
যেহেতু 3Ω ও 6Ω সমান্তরালে অবস্থান করছে সেহেতু Norton Resistance হবে,
RN = 3 ।। 6
⇒ RN = (3 × 6) / (3 + 6)
⇒ RN = 18 / 9
.’. RN = 2 Ω
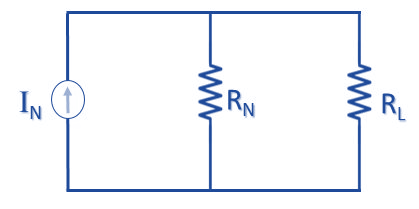
সুতরাং Norton’s Equivalent Circuit হবে নিম্নরুপঃ
বেসিক সূত্র সমূহ পড়ুনঃ
ওহমের সূত্র নিয়ে বিস্তারিত আলোচনা
সুপারপজিশন থিওরেম সম্বন্ধে বিস্তারিত পড়ুন।
