আজ আমরা আলোচনা করবো ট্রান্সফার ফাংশন (Transfer Function) নিয়ে। কন্ট্রোল সিস্টেমের প্রতিটা টপিকেই ট্রান্সফার ফাংশনের সমীকরণ রয়েছে। তাই কন্ট্রোল সিস্টেম ভালো করে জানা ও বুঝার পূর্বশর্ত হচ্ছে ট্রান্সফার ফাংশন ভাল করে জানা ও বুঝা।
এখন জেনে নেই আজ আমরা কি কি আলোচনা করতে যাচ্ছি-
- ট্রান্সফার ফাংশনের সংজ্ঞা।
- ট্রান্সফার ফাংশনের গাণিতিক রুপ।
- ট্রান্সফার ফাংশনের সমীকরণ কখন STRICTLY PROPER, PROPER ও IMPROPER হয়?
- ট্রান্সফার ফাংশনের ব্লক ডায়াগ্রাম।
- ট্রান্সফার ফাংশনের কার্যপ্রনালী।
- ট্রান্সফার ফাংশন এর characteristic equation.
১। ট্রান্সফার ফাংশন
একটি সিস্টেমের ট্রান্সফার ফাংশনকে আউটপুটের লেপলাস ট্রান্সফর্ম (Laplace Transform) এর সাথে ইনপুটের লেপলাস ট্রান্সফর্ম এর অনুপাত হিসাবে সংজ্ঞায়িত করা হয় যেখানে সব Initial Conditions শূন্য থাকে।
অর্থাৎ,
ট্রান্সফার ফাংশন = আউটপুটের লেপলাস ট্রান্সফর্ম : ইনপুটের লেপলাস ট্রান্সফর্ম
বা, ট্রান্সফার ফাংশন = আউটপুটের লেপলাস ট্রান্সফর্ম / ইনপুটের লেপলাস ট্রান্সফর্ম
ট্রান্সফার ফাংশন কন্ট্রোল সিস্টেমের আউটপুট সিগন্যাল সাথে সম্ভাব্য সকল ইনপুট মানের সম্পর্ক Represent করে থাকে।
২। ট্রান্সফার ফাংশনের গাণিতিক রুপঃ
আমরা এবার ট্রান্সফার ফাংশনের গাণিতিক রুপ বর্ণনা করবো। এ ক্ষেত্রে প্রথমে আমরা ইনপুটকে r(t) এবং আউটপুটকে c(t) ধরে নেই। এবার Linear system এর আলোকে ইনপুট-আউটপুটের n তম পদের Differential Equation করি-
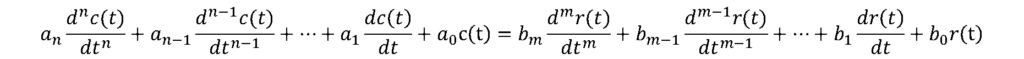
……………সমীকরণ ১.১
এখানে, a ও b হচ্ছে Constant বা ধ্রুবক
সমীকরণ ১.১ কে লেপলাস ট্রান্সফর্ম এ রূপান্তর করি –
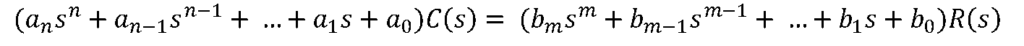
…………… সমীকরণ ১.২
সুতরাং এবার আমরা ট্রান্সফার ফাংশনকে নিম্ন লিখিতভাবে লিখতে পারি,
G (s) = C (s) / R (s)
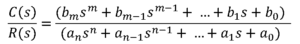
…………… সমীকরণ ১.৩
৩। ট্রান্সফার ফাংশনের সমীকরণ কখন STRICTLY PROPER, PROPER ও IMPROPER হয়?
সমীকরণ ১.৩ এর হর যদি লবের চেয়ে বড় হয় তখন ট্রান্সফার ফাংশনকে বলা হয় STRICTLY PROPER. আবার যদি লব ও হর উভয়ই এক সমান হয় তখন ট্রান্সফার ফাংশনকে বলা হয় PROPER এবং লব যখন হরের চেয়ে বড় হয় তখন ট্রান্সফার ফাংশনকে বলা হয় IMPROPER.
৪। ট্রান্সফার ফাংশনের ব্লক ডায়াগ্রাম
চলুন এবার একটি ব্লক ডায়াগ্রামের সাহায্যে ট্রান্সফার ফাংশনকে বোঝার চেষ্টা করিঃ

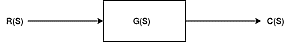
উপরের ব্লক ডায়াগ্রামকে ওপেন লুপ সিস্টেমের আলোকে বিবেচনা করলে
এখানে,
C(S)= আউটপুটের লেপলাস ট্রান্সফর্ম
R(S) = ইনপুটের লেপলাস ট্রান্সফর্ম
G(S) = ট্রান্সফার ফাংশন
ব্লক ডায়াগ্রাম হতে আমরা ট্রান্সফার ফাংশনকে নিম্মরুপে প্রকাশ করতে পারি,
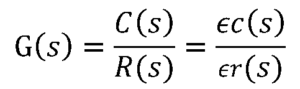
৫। ট্রান্সফার ফাংশনের কার্যপ্রনালী
ট্রান্সফার ফাংশন নির্ণয় করার জন্য চারটি ধাপ বা Steps রয়েছে।
- ১ম ধাপ: এই ধাপে আমরা প্রদত্ত সিস্টেম এর Differential Equation লিখবো।
- ২য় ধাপঃ ১ম ধাপ থেকে প্রাপ্ত Equation কে লেপলাস ট্রান্সফর্ম করে নিবো। এবং লেপলাস ট্রান্সফর্ম করার সময় initial Condition শুন্য ধরে নিতে হবে।
- ৩য় ধাপঃ এই ধাপে আমাদেরকে ২য় ধাপে প্রাপ্ত লেপলাস ট্রান্সফর্ম হতে ইনপুট ও আউটপুট এর অনুপাত বের করে নিতে হবে।
- ৪র্থ ধাপঃ ৩য় ধাপ হতে প্রাপ্ত Equation কে সিস্টেমের ট্রান্সফার ফাংশনে রূপান্তর করতে হবে।
অর্থাৎ G (s) = C (s) / R (s) আকারে প্রকাশ করতে হবে।
৬। ট্রান্সফার ফাংশন এর characteristic equation
ট্রান্সফার ফাংশন এর characteristic equation বের করার জন্যে আমারা linear system এর characteristic equation নিবো। এরপর linear system এর characteristic equation হতে প্রাপ্ত সমীকরণের আলোকে ট্রান্সফার ফাংশনের বহুপদী হরকে শূন্য করে দিবো। বহুপদী হরকে শূন্য করার পর আমারা যে সমীকরণটি পাবো সেটাই হচ্ছে ট্রান্সফার ফাংশন এর characteristic equation। ট্রান্সফার ফাংশনের characteristic equation নিচে দেওয়া হলোঃ
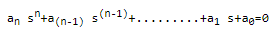
লক্ষ্যনীয় বিষয়ঃ
ট্রান্সফার ফাংশন পড়ার সময় আমরা অবশ্যই খাতা কলম সাথে নিবো, প্রতিটা সমীকরণ স্টেপ বাই স্টেপ খাতায় তুলে বোঝার চেষ্টা করবো। অন্যথায় আমরা যদি শুধু দেখে দেখে পড়ে যাই তাহলে পরবর্তীতে খুব সহজেই ভুলে যাবার সম্ভাবনা আছে। আজ এ পর্যন্তই। আল্লাহ হাফেজ.