থেভেনিন’স থিওরেম | Thevenin’s Theorem

কমপ্লেক্স সার্কিট সমাধান করার একটি জনপ্রিয় পদ্ধতি হলো থেভেনিন থিওরেম। ১৮৮৩ সালে ফরাসি টেলিগ্রাফ ইঞ্জিনিয়ার লিওন চার্লস থেভেনিন (Léon Charles Thévenin) এই থিওরেমটি আবিষ্কার করেন। কিন্তু ১৯২৬ সালের দিকে জানা যায় যে, জার্মান বিজ্ঞানী হারমান ভন হেল্মহোল্টজ (Hermann von Helmholtz) ১৮৫৩ সালে এই একই তত্ত্ব আবিষ্কার করেছিলেন। কিন্তু ততোদিনে এই থিওরেমটি থেভেনিন থিওরেম হিসেবে ব্যাপক জনপ্রিয়তা লাভ করে ফেলেছে।

আজকে আমরা থেভেনিন থিওরেম সম্বন্ধে বিস্তারিত আলোচনা করবো। আমাদের আজকের আলোচনায় যা যা থাকছেঃ  

• থেভেনিন থিওরেম বিবৃতি।
• থেভেনিন থিওরেম সম্বন্ধে প্রাথমিক জ্ঞান।
• থেভেনিন থিওরেম এর প্রয়োজনীয়তা।
• থেভেনিন থিওরেম প্রয়োগ করার ধাপ সমূহ।
• থেভেনিন থিওরেমের সাহা্য্যে সার্কিট সমাধান (গানিতিক)।

ইলেকট্রিক্যালের প্রয়োজনীয় কিছু সূত্র যা আপনার জেনে রাখা উচিত

থেভেনিন’স থিওরেম বিবৃতিঃ

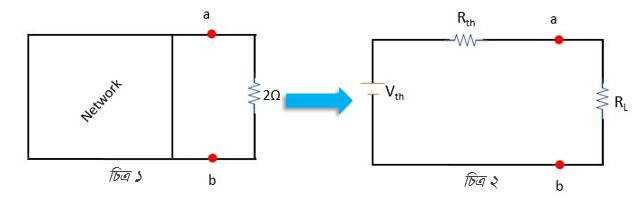
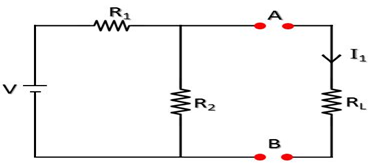
থেভেনিন তার থিওরেমে বলেন, একটি নেটওয়ার্ক সার্কিটের ভেতর (চিত্র ১) যতো কম্পোনেন্টই থাকুক না কেনো তা যদি টু টার্মিনাল নেটওয়ার্ক এবং লিনিয়ার বাই লেটারাল সার্কিট হয় তবে তা একটি ভোল্টেজ সোর্স ও সিরিজ রেজিস্ট্যান্স দ্বারা প্রকাশ করা যায় (চিত্র ২)।

যেকোন দুই টার্মিনাল লিনিয়ার নেটওয়ার্ক বা সার্কিটকে একটি Equivalent Network / Circuit আকারে প্রকাশিত করা যেতে পারে যা একটি রেজিস্টর ভোল্টেজ সোর্সের সাথে সিরিজে থাকবে। এটাকে মূলত Thevenin’s equivalent Circuit বলা হয়। একটি লিনিয়ার সার্কিটে Independent source, dependent source, এবং রেজিস্টর থাকতে পারে।  

থেভেনিন থিওরেম সম্বন্ধে প্রাথমিক জ্ঞানঃ

থেভেনিন থিওরেমের সাহায্যে কোন সার্কিট সমাধান করার পূর্বে আমাদেরকে কিছু বিষয় মনে রাখা একান্ত জরুরী যেমন, যখন থেভেনিন সার্কিট হতে ভোল্টেজ সোর্স ও কারেন্ট সোর্স খুলে সার্কিটের মোট রেজিস্ট্যান্স হিসাব করা হয় তখন এই মোট রেজিস্ট্যান্সকে বলা হয় থেভেনিন রেজিস্ট্যান্স যা R_th দ্বারা প্রকাশ করা হয় এবং মোট ভোল্টেজকে বলা হয় থেভেনিন ভোল্টেজ যা V_th দ্বারা প্রকাশ করা হয়। এই থেভেনিন ভোল্টেজ ও থেভেনিন রেজিস্ট্যান্স একত্রিত করলে থেভেনিন সার্কিট পাওয়া যায়। এছাড়াও থেভেনিন সার্কিটে সাধারণ রেজিস্টর বা অন্য কোন ডিভাইস লোড রেজিস্টর হিসেবেও কাজ করে, যা সার্কিট হতে শক্তি শোষন করতে পারে।

থেভেনিন থিওরেম এর প্রয়োজনীয়তাঃ

অনেক ক্ষেত্রে সার্কিট সমাধান করার সময় আমাদেরকে সার্কিট হতে লোড রেজিস্ট্যান্স বা কিছু Elements পরিবর্তন করতে হয়। কিন্তু যখন সার্কিট হতে কোন একটা Element বা লোড রেজিস্ট্যান্স পরিবর্তন করা হয় তখন পুরো সার্কিটটি পরিবর্তিত হয়ে যায়। যার ফলে আমাদেরকে প্রতিবারই নতুন করে সার্কিটটি সমাধান করতে হয় কিন্তু বারবার প্রতিটা সার্কিটে নতুন করে KVL, KCL, ওহম’স ল বা অন্য কোন সূত্র প্রয়োগ করা অনেক সময় সাপেক্ষ এবং ঝামেলার ব্যাপার।

তাই আমরা থেভেনিন থিওরেম ব্যবহার করে ঐ সার্কিটকে সিম্পল সিরিজ সার্কিটে রুপান্তর করে খুব সহজেই সমাধান করতে পারি। যেহেতু সার্কিটটি সিরিজে থাকে সেহেতু লোড রেজিস্ট্যান্স বা কোন Element পরিবর্তন করতে তেমন কোন অসুবিধায় হয় না।

থেভেনিন থিওরেম প্রয়োগ করার ধাপ সমূহঃ

থেভেনিন থিওরেম এর সাহায্যে কোন সার্কিটকে সমাধান করতে হলে আমাদেরকে কিছু ধাপ বা Steps অনুসরণ করতে হয়। নিম্নে তা ব্যাখ্যাসহ দেওয়া হলোঃ

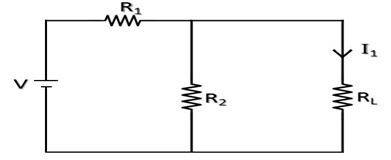
Step 1: যে রেজিস্ট্যান্স এর কারেন্ট নির্ণয় করতে হবে সার্কিট হতে সেই রেজিস্ট্যান্স খুলে আলাদা নিতে হবে। (সার্কিট ২)

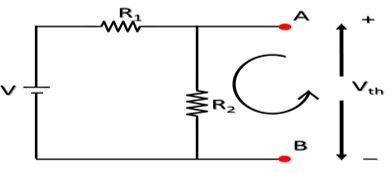
Step 2: সার্কিটে লুপ চিহ্নিত করে লুপে কার্শফের ভোল্টেজ সূত্র (KVL) প্রয়োগ করে যে রেজিস্ট্যান্স খোলা হয়েছে তা থেকে থেভেনিন ভোল্টেজ (V_th) নির্ণয় করতে হবে।

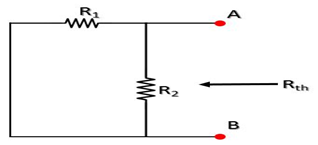
Step 3: সকল ভোল্টেজ সোর্সগুলো শর্ট করে দিতে হবে এবং কারেন্ট সোর্সগুলো ওপেন করে ঐ খোলা প্রান্ত হতে থেভেনিন রেজিস্ট্যান্স (R_th) নির্ণয় করতে হবে (সার্কিট ৪)। কিন্তু ভোল্টেজ সোর্সে ইন্টারনাল রেজিস্ট্যান্স থাকলে তা ভোল্টেজ সোর্সের স্থলে যুক্ত করতে হবে।

থেভেনিন রেজিস্ট্যান্স, R_th = (R₁ R₂) / (R₁ + R₂)

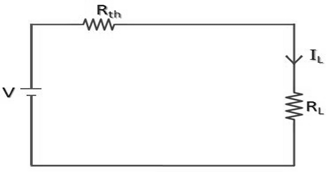
Steps 4: সর্বশেষ আমাদেরকে V_th, R_th ও R_L এর সমন্বয়ে একটি Thevenin Equivalent Circuit অংকন করতে হবে এবং এই সার্কিট হতে লোড কারেন্ট (I_L) এর মান নির্ণয় করতে হবে। (সার্কিট ৫)

লোড কারেন্ট, I_L = V_th / (R_th + R_L)

থেভেনিন থিওরেমের সাহায্যে সার্কিট সমাধান (গানিতিক):

প্রশ্নঃ নিম্নে উল্লেখিত সার্কিট হতে থেভেনিন থিওরেম ব্যবহার করে সার্কিটের R রেজিস্ট্যান্সের মধ্য দিয়ে কি পরিমাণ কারেন্ট I প্রবাহিত হবে তা নির্নয় কর?

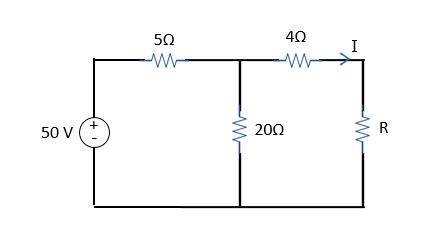
সমাধানঃ

যেহেতু আমাদেরকে R রেজিস্ট্যান্সের মধ্য দিয়ে কি পরিমাণ কারেন্ট প্রবাহিত হচ্ছে তা নির্ণয় করতে হবে সেহেতু আমরা এই লোডটি খুলে আলাদা করে নিতে হবে।

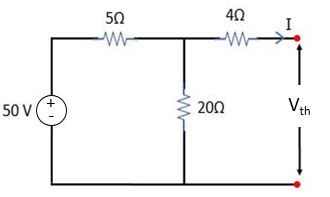
এবার সার্কিট হতে থেভেনিন ভোল্টেজ (V_th) নির্ণয় করতে হবে।

যেহেতু ডান পাশের প্রান্ত খোলা রয়েছে সেহেতু 4 Ω রেজিস্ট্যান্সে কোন কারেন্ট প্রবাহিত হবে না। তাই I = 0 হবে।

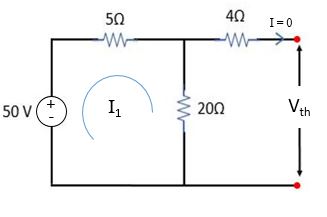
এবং 50 V , 5 Ω ও 20 Ω মিলে একটি সার্কিট পাবো। যদি আমরা এই সার্কিটের কারেন্টকে I₁ ধরি (সার্কিট ১.৩) তাহলে এর মান হবে, I₁ = 50 / (5+20) = 50 / 25 = 2 A.

যেহেতু এই সার্কিটে 2 A কারেন্ট প্রবাহিত হচ্ছে তাই 20 Ω এর across এ ভোল্টেজ হবে 2×20 V = 40 V

এবার আমাদেরকে KVL apply করে V_th এর মান বের করতে হবে,

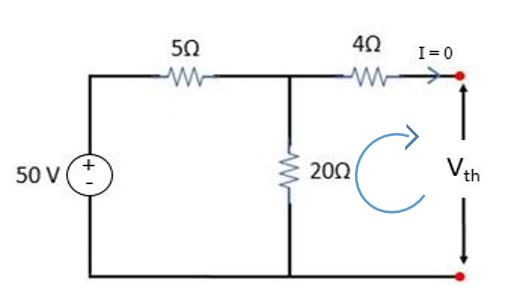
Applying KVL,

V_th – (I₁× R₃)+ (I × R₂)

⇒ V_th – 40 + (0×4) = 0

⇒ V_th – 40 + 0 = 0

.·. V_th = 40 V

এবার সার্কিটের ভোল্টেজ সোর্সকে শর্ট করে দিয়ে খোলা প্রান্ত হতে থেভেনিন রেজিস্ট্যান্স (R_th) নির্ণয় করতে হবে (সার্কিট ১.৫ )।

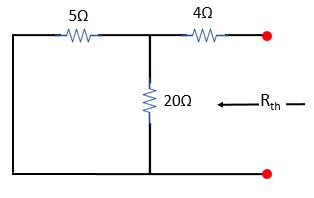
R_th = 5 ।। 20 + 4

⇒ R_th = {(5 x 20) / (5 + 20)} + 4

Or, R_th = (100 / 25) + 4

Or, R_th = 4 + 4

.·. R_th = 8 Ω

এবার আমাদেরকে V_th ও R_th এর সমন্বয়ে Thevenin Equivalent Circuit হবে,

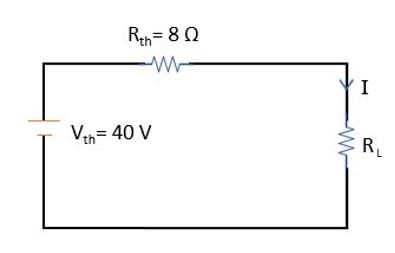
সুতরাং, R রেজিস্ট্যান্সের মধ্য দিয়ে প্রবাহিত কারেন্টের পরিমাণ,

I = 40 / (8 + R)

বেসিক সূত্র সমূহ পড়ুনঃ

ওহমের সূত্র নিয়ে বিস্তারিত আলোচনা

কার্শফের কারেন্ট সূত্র (KCL)

কার্শফের ভোল্টেজ সূত্র (KVL)