থ্রি ফেজ ইলেকট্রিক সার্কিট এনালাইসিসে বহুল ব্যবহৃত একটি রূপান্তর পদ্ধতি হলো স্টার ডেল্টা রুপান্তর। এছাড়া এমন কিছু জটিল সার্কিট আছে যা সিরিজ সার্কিট নাকি প্যারালাল সার্কিট তা নির্ণয় করা কঠিন হয়ে পড়ে সে ক্ষেত্রে স্টার ডেল্টা রূপান্তর করে খুব সহজেই জটিল সার্কিটকে সমাধান করা যায়।
আজ আমরা স্টার সংযোগ হতে ডেল্টা সংযোগ ও ডেল্টা সংযোগ হতে স্টার সংযোগে রূপান্তর পদ্ধতি নিয়ে বিস্তারিত আলোচনা করব।
আমাদের আজকের আলোচনায় যা যা থাকছেঃ
- ভূমিকা।
- স্টার সংযোগ কি?
- ডেল্টা সংযোগ কি?
- স্টার সংযোগ হতে ডেল্টা সংযোগে রুপান্তরের পদ্ধতি।
- ডেল্টা সংযোগ হতে স্টার সংযোগে রুপান্তরের পদ্ধতি।
ভূমিকাঃ
১৮৯৯ সালে আর্থার এডউইন কেনেলি (Arthur Edwin Kennelly) সার্কিট রূপান্তরের এই তত্ত্বটি প্রথম প্রকাশ করেছিলেন।
স্টার-ডেল্টা রূপান্তরটি বিভিন্ন নামে পরিচিত যেমনঃ ওয়াই-ডেল্টা (Y-Δ) রূপান্তর, স্টার-মেশ রূপান্তর, টি-পাই (T-Π) রূপান্তর। এই রুপান্তর পদ্ধতি স্টার ডেল্টা বা ওয়াই ডেল্টা রূপান্তর হিসেবে বেশি পরিচিত। সার্কিট ডায়াগ্রামের আকারের উপর ভিত্তি করে এসব নামকরণ করা হয়। উল্লেখ্য যে, ফিনল্যান্ডের ভাষায় Y কে স্টার বলা হয়। আমরা আমাদের আলোচনায় স্টার ও ডেল্টা শব্দ ব্যবহার করব।
স্টার সংযোগ কি?
যে সংযোগে কন্ডাকটর সমূহের রেজিস্ট্যান্স গুলো একটি নির্দিষ্ট বিন্দুতে সংযুক্ত থাকে তাকে স্টার সংযোগ বলা হয়।
নিম্নে একটি স্টার সংযোগ দেখানো হলোঃ
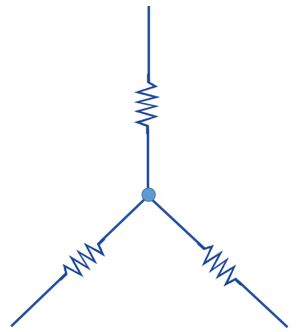
ডেল্টা সংযোগ কি?
যে সংযোগে কন্ডাকটর সমূহের রেজিস্ট্যান্স গুলো ত্রিভুজ আকৃতিতে সংযুক্ত থাকে তাকে ডেল্টা সংযোগ বলা হয়।
নিম্নে একটি ডেল্টা সংযোগ দেখানো হলোঃ
স্টার সংযোগ হতে ডেল্টা সংযোগে রুপান্তরের পদ্ধতিঃ
স্টার সংযোগ হতে পর্যায়ক্রমে দুইটি রেজিস্ট্যান্স গুণ করে সেই রেজিস্ট্যান্সগুলো পরস্পর যোগ করে যোগফলকে ডেল্টার যে রেজিস্ট্যান্স নির্ণয় করবো তার বিপরীত পাশে স্টার সংযোগের যে রেজিস্ট্যান্স থাকবে তা দ্বারা ভাগ করতে হবে।
উদাহরণঃ
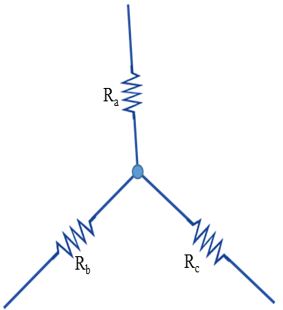
Ra, Rb ও Rc রেজিস্ট্যান্স যুক্ত একটি স্টার সংযোগ দেওয়া আছে। এই সংযোগকে ডেল্টায় রূপান্তর করতে হবে।
রূপান্তর করার জন্য আমরা প্রথমে স্টার সংযোগের উপরে কাল্পনিকভাবে একটি ডেল্টা সংযোগ অংকন করে নিলাম।
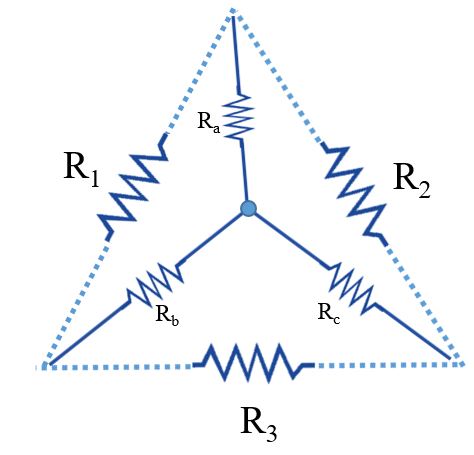
এবার উপরোক্ত পদ্ধতি অনুযায়ী আমরা যদি, R1, R2 ও R3 নির্ণয় করি তাহলে প্রথমে আমাদেরকে স্টার সংযোগ হতে পর্যায়ক্রমে দুইটি রেজিস্ট্যান্স একত্রে গুণ করে তাদেরকে যোগ করব।
অর্থাৎ, RaRb + RbRc + RcRa
যেহেতু আমরা R1 নির্ণয় করতেছি সেহেতু R1 এর বিপরীতে অবস্থিত স্টার সংযোগের রেজিস্ট্যান্স Rc দ্বারা RaRb + RbRc + RcRaভাগ করব।
অতএব R1 এর সমীকরণটি হচ্ছে,
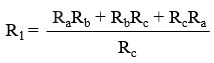
একই ভাবে R2 ও R3 এর সমীকরণ হবে,
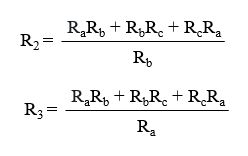
গাণিতিক সমস্যা সমাধানের ক্ষেত্রে উপরোক্ত পদ্ধতিতে Ra, Rb ও Rc এর স্থলে প্রশ্নে উল্লেখিত মান বসিয়ে খুব সহজেই স্টার সংযোগকে ডেল্টা সংযোগে রুপান্তর করতে পারি।
ডেল্টা হতে স্টার সংযোগে রুপান্তরের পদ্ধতিঃ
ডেল্টা সংযোগের একটি নির্দিষ্ট প্রান্তে সংযুক্ত দুইটি ডেল্টা রেজিস্ট্যান্স এর গুনফলকে সংযোগে অবস্থিত তিনটি রেজিস্ট্যান্স এর যোগফল দ্বারা ভাগ করতে হবে।
উদাহরণঃ
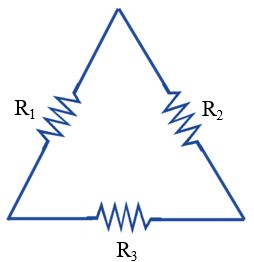
R1, R2 ও R3 রেজিস্ট্যান্স যুক্ত একটি ডেল্টা সংযোগ দেওয়া আছে। এই সংযোগকে স্টারে রূপান্তর করতে হবে।
রূপান্তর করার জন্য আমরা প্রথমে ডেল্টা সংযোগের ভিতরে কাল্পনিকভাবে একটি স্টার সংযোগ অংকন করে নিলাম।
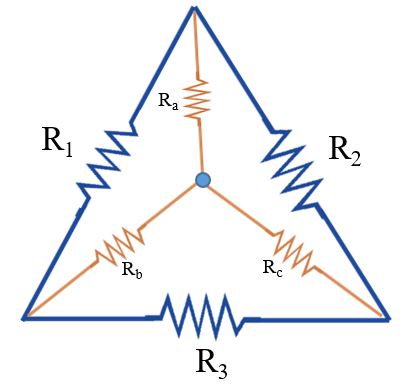
এবার উপরোক্ত পদ্ধতি অনুযায়ী আমরা Ra, Rb ও Rc নির্ণয় করব।
যদি Ra নির্ণয় করতে চাই তাহলে এর সাথে সংযুক্ত দুইটি ডেল্টা রেজিস্ট্যান্স R1 ও R2 এর গুনফলকে রেজিস্ট্যান্স ৩ টি R1, R2 ও R3 এর যোগফল দ্বারা ভাগ করতে হবে।
অর্থাৎ,
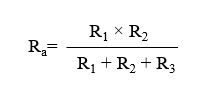
একইভাবে,
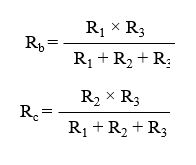
গাণিতিক সমস্যা সমাধানের ক্ষেত্রে উপরোক্ত পদ্ধতিতে R1, R2 ও R3 এর স্থলে প্রশ্নে উল্লেখিত মান বসিয়ে খুব সহজেই ডেল্টা সংযোগকে স্টার সংযোগে রুপান্তর করতে পারি।
বেসিক সূত্র সমূহ পড়ুনঃ
ওহমের সূত্র নিয়ে বিস্তারিত আলোচনা।
কার্শফের কারেন্ট সূত্র (KCL) সম্বন্ধে বিস্তারিত পড়ুন।
কার্শফের ভোল্টেজ সূত্র (KVL) সম্বন্ধে বিস্তারিত পড়ুন।
সুপারপজিশন থিওরেম সম্বন্ধে বিস্তারিত পড়ুন।
থেভেনিন’স থিওরেম সম্বন্ধে বিস্তারিত পড়ুন।
